Copyright
2020 Robert Clark
(patents
pending)
I.)Introduction.
The origin of this research is
from an argument I once made as a point of scientific philosophy:
Is it reasonable that an
equation of physics should be considered to be *exactly* true for the entire
future of physics? Since we are not at the stage of having a final theory I
don't think that is likely.
I made this point 20 years ago
on various online science forums in regard to the Lorentz transformations, vis
a vis special relativity:
From: rgc...@my-deja.com (Robert Clark)
Newsgroups:
sci.physics,sci.physics.relativity,sci.astro,sci.math
Subject: Re : Are Neutrinos tachyons?
Date: 11 Jul 2001 19:26:32 -0700
Organization: http://groups.google.com/
ba...@galaxy.ucr.edu (John Baez) wrote in
message
news: <9i8a1n$ej2$1...@glue.ucr.edu> ...
> In
article
<3uqakt8021vp6mv3j...@4ax.com> ,
>
Zed
<bad@nowhere.don'tspam.me.com>
wrote:
> >
I've read that tachyonics are usually the sign that a ground state
> >
of the vacuum has not correcly been identified. Would tachyonic
> >
neutrinos mean that our universe is only metastable against vacuum
> >
decay?
>
>
Worse: unstable! A more lowbrow way
of putting this is that the
>
existence of tachyons would allow to create something like
> a
perpetual motion machine. Tachyons can
go faster than light,
> and
anything going faster than light will look like it's going
> backwards
in time when viewed in a suitably moving inertial
>
reference frame.
> ...
An
interesting question: is the reason why physicists continue to say
that superluminal travel would require causality
violations because
they are CERTAIN that the alternative of a
preferred frame is not the
case or is it because it is simply not discussed
as a possibility in
physics courses and textbooks?
In any
case it seems to me those who are aware of it should at least
mention that it is an alternative possibility to
the idea that
superluminal speeds imply travel back in time.
Note also
that negative energy states are an inherent part of quantum
field theory, and "Casimir regions"
would be small areas where such
states are stable. Indeed the recent
experimental confirmations of the
Casimir effect suggest that the energy state of
a Casimir region is
below the standard vacuum value and it is
stable.
__________________________________________________________
From: Robert Clark (rgc...@my-deja.com)
Subject: Re: Faster Than Light in our lifetime?
Newsgroups: sci.space.tech, sci.space.science
Date: 2001-06-04 22:45:41 PST
jth...@galileo.thp.univie.ac.at (Jonathan
Thornburg) wrote in message news:
<9f2kd7$401$1...@mach.thp.univie.ac.at>
...
> In
article <9f1k2o$ok8$1...@iac5.navix.net>
,
>
Robert Miller
<star...@alltel.net> wrote:
> >
What is the chance of FTL travel in our lifetime?
>
>
Almost all physicists would say "very small".
>
> The
problem is that even FTL *signalling* (never mind FTL travel)
>
creates severe problems with causality:
If you could send a signal
>
faster than light, then by sending a suitable out-and-return pair of
>
signals between two rapidly (but still slower-than-light) moving
>
spaceships, you could arrange to have the return signal arrive back
> from
its overall out-and-return journey *before* you sent it!
>
> ...
Actually
it is known that faster than light speeds really would not
require causality violations. What it would
require is a preferred
frame:
**************************************************
From: Robert Clark (rgc...@my-deja.com)
Subject: Re: Ftl on the horizon???
Newsgroups: rec.arts.sf.science
Date: 2000/06/08
In article
<13989-39...@storefull-158.iap.bryant.webtv.net> ,
jjI...@webtv.net (JJ) wrote:
>
A friend sent me the article below It looks like ftl and time
>
travel might be possible after all. Just think another example of
"it
>
can't be done" being done. Whats the next thing that can't be done
going
> to
be I wonder, the nay sayers still abound.
>
> THE
SUNDAY TIMES: FOREIGN NEWS
>
Address:http://www.sunday-
times.co.uk/news/pages/sti/2000/06/04/stifgnusa01007.html
>
Changed:1:20 PM on Sunday, June 4, 2000
>
> jj
>
>
It has
been known since at least the 1930's with the publication of
the German edition of Reichenbach's _The
Philosophy of Space and Time_
that superluminal signaling need not require
causality violations.
This is because, as Reichenbach noted, it is a
matter of convention that
the *one-way* speed of light is a constant c.
The experimental results of
relativity may just as well be explained by
assuming the speed of
light is slowed in one direction and
correspondingly speeded-up in the
other. This does not require travel back in time,
but it would require
a need for a preferred frame.
This is
well known among researchers in the foundations of relativity
but does not seem to have filtered down among
physicists in general,
as indicated by the descriptions of these recent
experiments:
physics : Faster than light
Light Exceeds Its Own Speed Limit, or Does it?
Eureka! Scientists break speed of light
One of
the few times I've seen a mainstream physicist comment that
superluminal signaling would require a preferred
frame and not travel
back in time or causality violations was from
CERN physicist Alexander
Kusenko in discussing a theory that the
explanation of the "solar
neutrino deficit" was due to a superluminal
speed of neutrino:
"One objection is that if tachyons exist,
they could be used for
faster-than-light communication, causing curious
reversals of cause and
effect. Rembielinski says this can be avoided,
but only by abandoning
the "relativity principle", which
requires that the laws of physics
look the same to all observers moving at a
constant speed relative to
each other."
"Dumping the relativity principle means
accepting that one frame in
theUniverse is special," says Alexander
Kusenko of CERN, the European
particle physics laboratory in Geneva.
"It's aesthetically displeasing
and it makes physics messy." He suspects
that the tritium experiments
indicate an imaginary mass for the neutrino only
because of
experimental uncertainties."
Speed freaks.
New Scientist, 16 August, 1997
I don't
agree here that a preferred frame would necessarily make
physics more complicated. That presupposes that
this preferred frame
would be difficult to detect. If arbitrarily
high speeds could be
achieved, then it is possible that absolute
simultaneity and absolute
time could also be determined. This might in
fact lead to the
unification of physics that has so far been
elusive.
The
possibility of superluminal speeds, and the fact this implies a
preferred frame, has also been investigated by
Harvard physicists
Sidney Coleman and Sheldon Glashow:
Cosmic Ray and Neutrino Tests of Special
Relativity
Authors: Sidney Coleman, Sheldon L. Glashow
Comments: 7 pages, harvmac, 2nd revision
discusses recent indications
of anisotropy of photons propagating over
cosmological distances and
is otherwise clarified. Report-no: HUTP-97/A008
Journal-ref: Phys.Lett. B405 (1997) 249-252
Searches for anisotropies due to Earth's motion
relative to a
preferred frame --- modern versions of the
Michelson-Morley experiment
---
provide precise verifications of special
relativity. We describe other
tests, independent of this motion, that are or
can become even more
sensitive. The existence of high-energy cosmic
rays places strong
constraints on Lorentz non-invariance.
Furthermore, if the maximum
attainable speed of a particle depends on its
identity, then
neutrinos, even if massless, may exhibit flavor
oscillations. Velocity
differences far smaller than any previously
probed can produce
characteristic
effects at accelerators and solar neutrino experiments.
Sheldon
Glashow is well known for his Nobel prize for the early
development of quantum chromodynamics(QCD) and
quantum electrodynamics
(QED). The number of physicists currently active
who know as much
about high-energy physics as Glashow can
probably be counted on one hand.
Since he has written several articles suggesting
that superluminal
speeds may explain certain experimental
anomalies I take it this is
not mere speculation for him, but rather he
considers it to be a real
possibility.
Some
articles discussing the fact that the constancy of the one-way
speed of light is a convention are:
Conventionality of Simultaneity
The Speed of Light - A Limit on Principle?
Relativizing Relativity
Two
papers by Winnie develop in detail a theory of relativity with a
varying speed of light:
Winnie, J. 1970a. "Special Relativity
Without One-Way Velocity
Assumptions: Part I," Philosophy of Science
37, 81-99.
Winnie, J. 1970b. "Special Relativity
Without One-Way Velocity
Assumptions: Part II," Philosophy of
Science 37, 223-238.
_______________________________________________
"In order for a scientific revolution to
occur,
most
scientists have to be wrong"
-- Bob Clark
_______________________________________________
*********************************************************
Also, in
my opinion, the mathematics and the experiments of modern
physics both suggest that Lorentz invariance
should be regarded as an
approximation at sufficiently high energies.
Below is an argument I
gave for this on the Slashdot.com site:
Re:Implications to relativity of the new
measureme (Score:2,
Interesting)
by rgclark on Sunday February 11, @03:26AM EST
(#14)
..
A key
point is philosophical/heuristic:
Is it
reasonable that an equation of physics should be considered to
be *exactly* true for the entire future of
physics? Since we are not
at the stage of having a final theory I don't
think that is likely.
However, note that the key idea that reaching
and exceeding the speed
of light would require infinite energy is based
on the idea that the
Lorentz transformation is *exactly* true, for if
not you don't get the
infinity by having a zero in the denominator.
One
might argue that in the future Lorentz invariance will be
replaced by a more accurate expression, but if
it will not be
*exactly* true at that time, surely it is not
*exactly* true now.
I
repeated this argument recently also in sci.physics.relativity and
received the response that the conservation of
energy is a
counterexample to the idea that a physical
equation should not be
considered to be exactly true. However,
remarkably, even conservation
of energy is dependent on Einstein's
transformation equations, so that
deviations from these will also have an effect on
how we interpret the
conservation of energy. This is discussed in one
of the papers that
discuss violations of Lorentz invariance. I'll
give you a reference if
you like. The possibility that conservation of
energy might also be
violated is probably even a more jarring idea
than that of violations
of Lorentz invariance.
The
mathematical reasons for doubting exact Lorentz invariance *for
real physical bodies* are these:
The equations of both quantum field theory and
general relativity have
been found to be analogous to those of fluid
mechanics. In fluid
mechanics we also have the fact that for the
approximate linear PDEs
describing the fluid, exceeding the wave speed
of the underlying
medium would result in an infinite pressure.
Naively, one might
conclude no body can exceed the speed of sound
in a medium. But of
course mathematicians and engineers know these
equations are
approximations. These linear PDEs need to be
replaced by the more
accurate nonlinear PDE's that describe the fluid
in transonic and
supersonic situations.
One
might take this to be just a coincidence that the most advanced
equations of modern physics, quantum field
theory and general
relativity, both describe the vacuum with
equations that are analogous
to those of a material medium. But the
predictions of those theories
are also what one would expect for a medium. In
quantum
electrodynamics and quantum field theory in
general we have the fact
that you must make mass and charge
renormalizations to describe the
reactions of subatomic particles very close to
the intense field of
the nucleus.
The key
fact about this in regard to this discussion is this: if
Lorentz invariance is to be true, then *every*
aspect of its
predictions must hold, not just simply time
transformations as
measured by decay rates. If the *intrinisic*
mass and charge have to
changed when moving at high speeds close to the
nucleus, then that
signals Lorentz invariance is not holding in
that situation. (Note
this is not the "relativistic mass"
change, and of course for Lorentz
invariance to hold, charge must be invariant.)
One
might say this is only true for subatomic particles close to the
nucleus, but the equations of QED show in fact
*this is true for a
field of any intensity*, the corrections are
just extremely small.
This is discussed in papers describing how the
speed of light is
altered in regions of strong electrical and
magnetic fields, which in
itself is telling you that the vacuum has
properties dependent on the
energy content in a region that effect the
*intrinisic* properties of
bodies in that region.
When I
had this discussion on sci.physics.relativity there was a
fundamentally important fact about this being
overlooked: not only do
mass and charge renormalizations have to be made
close to the nucleus,
but THE DEVIATIONS IN MASS AND CHARGE GET WORSE
AS THE SPEED OF THE
PARTICLE INCREASES. I can not overemphasize the
importance of this
fact to the argument. As I said before the mass
and charge
renomalizations are signals of the failure of
Lorentz invariance in
these situations. That the deviations get worse
with speed means the
deviation from Lorentz invariance gets worse
with speed. This is
exactly what you would expect if it were true
that this is analogous
to the situation of a body traveling through a
material medium and
that given sufficient energy you can exceed the
wave speed of the
medium.
As I
said the mathematics of general relativity also suggests
Lorentz invariance should only be an
approximation *for real physical
bodies*. In general relativity is it said
Lorentz invariance holds
only "locally". This is defined to
mean it only holds *at a point*, or
equivalently it holds on a tangent plane. But in
differential geometry
on which GR is based, a property is said to hold
locally, when it
holds *exactly* on a small region of the
manifold. According to
differential geometry which is the mathematical
theory deriving GR,
Lorentz invariance does not hold locally using
the definition used in
that theory and in every field of mathematics
that uses the concept of
a manifold. In the primary reference work on GR
_Gravitation_ by
Wheeler, Misner and Thorne it says explicitly
that in real space with
curvature, containing real bodies inducing their
own space-time
curvature Minkowski space can not be expected to
exactly hold. To me
this is saying that Lorentz invariance does not
hold exactly for real
physical bodies in real space with curvature.
In the
debates on sci.physics.relativity I only gave a heuristic
reason that I think can probably be made
rigorous that the
fundamentally important fact that the deviations
from Lorentz
invariance get worse as the speed of the body
increases also holds in
general relativity: the fact that the effective
"force" a body feels
becomes greater as the speed of the body
increases (this is discussed
in the FAQ for the sci.physics.relativity
group.) This suggests that
the *intrinsic* mass of the body is increasing
with speed. (Again this
is not the "relativistic mass"
correction.) However, I found an
article in the American Journal of Physics that
says this explicitly:
American Journal of Physics -- July 1985 --
Volume 53, Issue 7, pp.
661-663
Measuring the active gravitational mass of a moving
object
D. W. Olson and R. C. Guarino
Department of Physics, Southwest Texas State
University, San Marcos,
Texas 78666
If a heavy object with rest mass M moves past
you with a velocity
comparable to the speed of light, you will be
attracted
gravitationally towards its path as though it
had an increased mass.
If the relativistic increase in active
gravitational mass is measured
by the transverse (and longitudinal) velocities
which such a moving
mass induces in test particles initially at rest
near its path, then
we find, with this definition, that
Mrel=gamma(1+beta^2)M. Therefore,
in the ultrarelativistic limit, the active
gravitational mass of a
moving body, measured in this way, is not gammaM
but is approximately
2gammaM.
Note
this "effective" mass of the body in a gravitational field is
again not the simple "relativistic
mass". To me this is again
signaling that Lorentz invariance is only an
approximation for real
physical bodies.
Another
article in AJP that appears to be saying this is by Steve
Carlip:
American Journal of Physics -- May 1998 --
Volume 66, Issue 5, pp.
409-413
Kinetic energy and the equivalence principle
S. Carlip
Department of Physics, University of California,
Davis, California
95616
According to the general theory of relativity,
kinetic energy
contributes to gravitational mass. Surprisingly,
the observational
evidence for this prediction does not seem to be
discussed in the
literature. I reanalyze existing experimental
data to test the
equivalence principle for the kinetic energy of
atomic electrons, and
show that fairly strong limits on possible
violations can
be obtained. I discuss the relationship of this
result to the
occasional claim that "light falls with
twice the acceleration of
ordinary matter."
However,
I'm only judging here by the abstract as I haven't had the
chance to read this article yet. I also hasten
to add that Dr. Carlip
is a frequent contributor to the
sci.physics.relativity group in which
he argues against speeds surpassing the speed of
light, so he would
probably be opposed to the idea that Lorentz
invariance is only an
approximation.
These
articles can be found by searching on AJP's site:
http://ojps.aip.org/ajp/
Note I
am suggesting that high speeds and energy content in a region
can effect what are regarded as intrinsic
properties. This of course
implies these properties really are not
intrinsic but are dependent on
surrounding conditions. My view is that
properties such as mass and
charge will be found to be tensors dependent on
the mass/energy
distribution in their vicinity and indeed on
that of the universe.
Bob Clark
*************************************************************************
_____________________________
II.)Superluminal effects.
A remarkable phenomenon of quantum mechanics is
"quantum tunneling". This is an effect where an electron that
shouldn't have enough energy to pass through a barrier, can nevertheless show
up beyond it on the other side (whether or not it actually passed
through the barrier is another question.)
Even more remarkable experiments
show the transmission time is so short it may in fact be instantaneous:
Physicists measure quantum tunneling
time to be near-instantaneous.
By Michael Irving
March 18, 2019
Note though this is over very
short distances.
Another surprising effect in
quantum mechanics is the Scharnhorst effect. This takes place in a vacuum
between two conductive plates placed very close together. Calculations show the
energy density between the two plates should be reduced below that of the usual
vacuum:
Scharnhorst effect.
https://en.wikipedia.org/wiki/Scharnhorst_effect
Scharnhorst effect.
https://en.wikipedia.org/wiki/Scharnhorst_effect
The space between the plates is called a Casimir
region or a Casimir vacuum. It has been shown that in the Casimir vacuum the
reduced energy density between the plates results in an excess pressure in the
vacuum on the outside of the plates, pushing them together. This has now been
experimentally confirmed called the Casimir
Based on the concept of a
reduced energy density between the plates in the Casimir vacuum, Scharnhorst
calculated that the speed of light should be increased between the plates above
that of the usual vacuum value:
Science: Can photons travel 'faster
than light'?
7 April 1990
By Marcus Chown
This effect like quantum
tunneling takes place over extremely small distances, essentially atomic
lengths. This led to the conclusion that they could not be used in practice for
faster than light communication. But suppose we combined the two effects to get
superluminal signaling over long distances?
I imagine using nanotechnology
to construct a repeated array consisting of a quantum tunnelling plate flowed
by a pair of Casimir plates, with this pattern repeated to get a macroscale
communication fiber.
To get the quantum tunneling
effect the distance has to be in the range of 1 - 3 nm, and smaller:
Lerner; Trigg (1991). Encyclopedia
of Physics (2nd ed.). New York: VCH. p. 1308. ISBN 978-0-89573-752-6.
But even at plate separation
distance of 1 nm for a Casimir region the fractional increase in speed over the
standard speed of light by the Scharnhorst effect is only in the range of 1 part in 1020.
According to the equation, to get a very large light speed increase, the plate
distance would have be on the order of the proton diameter, ca. 10-15 m. See formulas here:
Faster-than-c signals, special relativity, and causality.
Stefano Liberati, Sebastiano Sonego, Matt Visser.
https://arxiv.org/pdf/gr-qc/0107091.pdf
This would be very difficult to achieve. Then instead I suggest Casimir plate wall separation on the order of an atomic diameter of an angstrom, 10-10 m. With the quantum tunneling walls being at 1 nm to 3 nm thick, the Casimir regions would be 1/10th to 1/30th as wide. Then if quantum tunnelling is indeed (near)instantaneous, even if the light speed in the Casimir regions is at standard c, the transmission time for the entire length of the fiber will be 1/10th to 1/30th that of the standard light speed value.
Faster-than-c signals, special relativity, and causality.
Stefano Liberati, Sebastiano Sonego, Matt Visser.
https://arxiv.org/pdf/gr-qc/0107091.pdf
This would be very difficult to achieve. Then instead I suggest Casimir plate wall separation on the order of an atomic diameter of an angstrom, 10-10 m. With the quantum tunneling walls being at 1 nm to 3 nm thick, the Casimir regions would be 1/10th to 1/30th as wide. Then if quantum tunnelling is indeed (near)instantaneous, even if the light speed in the Casimir regions is at standard c, the transmission time for the entire length of the fiber will be 1/10th to 1/30th that of the standard light speed value.
Still, it is a tantalizing
prospect to get the Casimir plate separation down to subatomic distances to get
multiple times higher light speed over standard c. One possibility is that the
Casimir effect tries to push the plates together at small distances, and the
effect gets stronger the closer the plates are.
Then we could have an ultra
high vacuum with only a few atoms at ca. 1 angstrom diameter between each pair
of Casimir plates. The Casimir force would compress the walls closer but still
kept separated by the few atoms between them. Perhaps we could get atoms of
compressed size this way.
Going a step further, perhaps
we could have individual protons keeping the walls separated but this time at
the 10-15 m proton diameter.
III.)Superconductivity.
The expectation is within a region of reduced energy density
such as a Casimir region electrons would have reduced resistance to flow as for
electricity transmission. And then the superluminal communication fibers would
also work as superconductors.
The phenomenon of "topological
insulators", where a material can be an insulator within its interior but
a conductor on its surface may be an instance of this phenomenon of alternating
quantum tunneling across walls and Scharnhorst superluminality between walls.
Quantum tunneling can as well
occur at small distances between plates, where electrons can
overcome an energy barrier to cross from one plate to the other:
Quantum
Conductivity.
While the Drude model of electrical conductivity makes excellent
predictions about the nature of electrons conducting in metals, it can be
furthered by using quantum tunnelling to explain the nature of the electron's
collisions.[24] When a free electron
wave packet encounters a long array of uniformly spaced barriers the
reflected part of the wave packet interferes uniformly with the transmitted one
between all barriers so that there are cases of 100% transmission. The theory
predicts that if positively charged nuclei form a perfectly rectangular array,
electrons will tunnel through the metal as free electrons, leading to an
extremely high conductance, and that impurities in the metal will
disrupt it significantly.[24]
This raises the possibility that
quantum tunneling is itself a superluminal phenomenon.
In any case, we want to
minimize the distance between the plates, even to subatomic distances. This may
be accomplished by methods now possible to individually manipulate atoms, such
as by using the Scanning Tunneling Microscope, STM. This can position atoms at
least to within an accuracy of 1 nm:
Then we can use the STM to
arrange the atoms in rectangular arrays. Some references give the resolution of
the STM as 0.001 nm, 1 picometer(pm):
SCANNING TUNNELING MICROSCOPE
The quantum
tunneling phenomenon at metallic surfaces, which we have just described, is the
physical principle behind the operation of the scanning tunneling microscope
(STM), invented in 1981 by Gerd Binnig and Heinrich Rohrer. The STM device
consists of a scanning tip (a needle, usually made of tungsten,
platinum-iridium, or gold); a piezoelectric device that controls the tip’s
elevation in a typical range of 0.4 to 0.7 nm above the surface to be scanned;
some device that controls the motion of the tip along the surface; and a
computer to display images. While the sample is kept at a suitable voltage
bias, the scanning tip moves along the surface (Figure 7.7.6) and the
tunneling-electron current between the tip and the surface is registered at
each position.
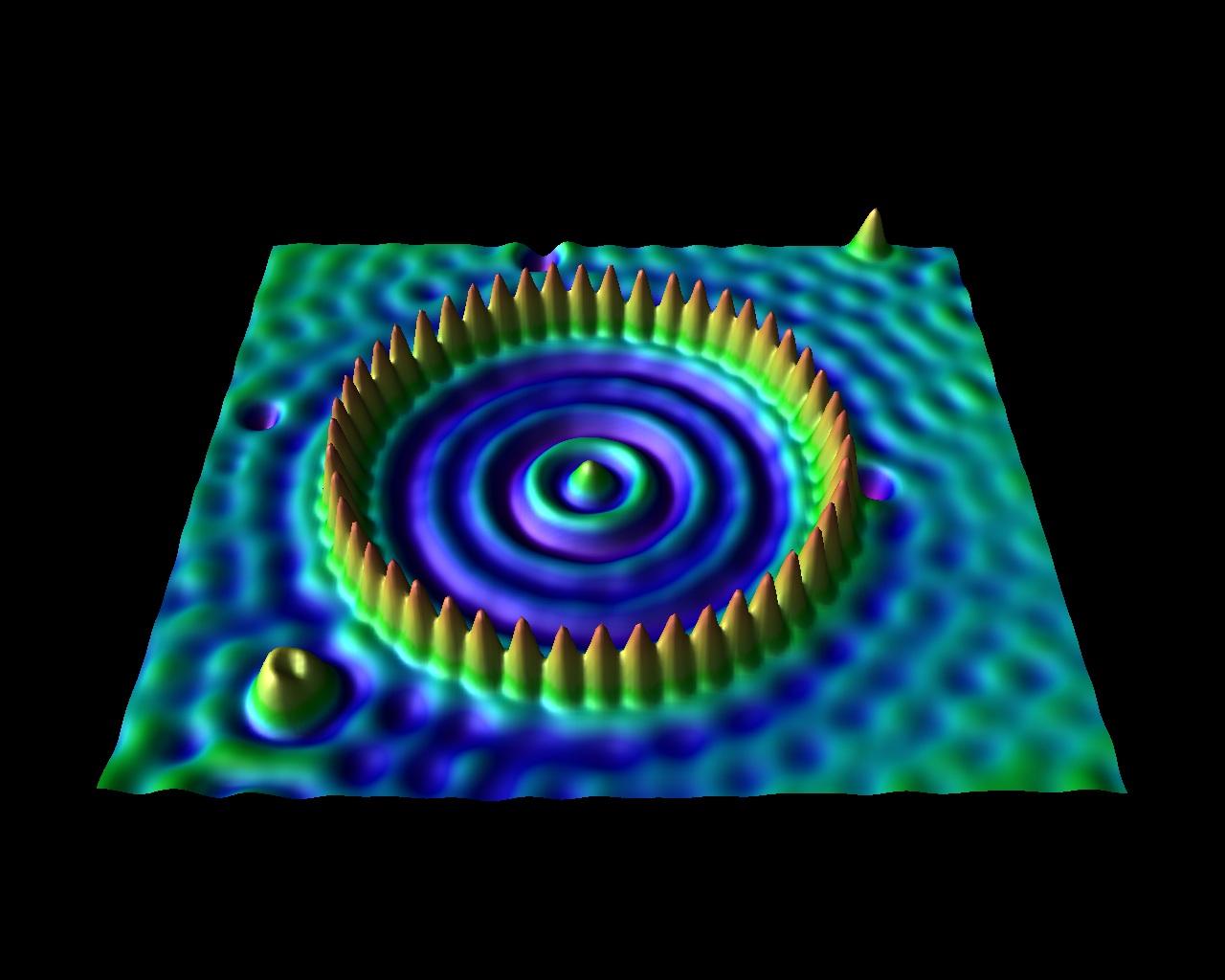
Figure 7.7.6: In STM, a surface at a constant potential is being
scanned by a narrow tip moving along the surface. When the STM tip moves close
to surface atoms, electrons can tunnel from the surface to the tip. This
tunneling-electron current is continually monitored while the tip is in motion.
The amount of current at location (x,y) gives information about the elevation
of the tip above the surface at this location. In this way, a detailed
topographical map of the surface is created and displayed on a computer
monitor.
The amount of the
current depends on the probability of electron tunneling from the surface to
the tip, which, in turn, depends on the elevation of the tip above the surface.
Hence, at each tip position, the distance from the tip to the surface is
measured by measuring how many electrons tunnel out from the surface to the
tip. This method can give an unprecedented resolution of about 0.001 nm, which
is about 1% of the average diameter of an atom. In this way, we can see
individual atoms on the surface, as in the image of a carbon nanotube in
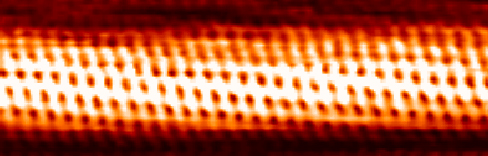
Figure 7.7.7.
Figure 7.7.7: An STM image of a carbon nanotube: Atomic-scale
resolution allows us to see individual atoms on the surface. STM images are in
gray scale, and coloring is added to bring up details to the human eye.
However, the STM having a
resolution of 1 pm doesn't mean it would have the positional placement accuracy
of atoms to that degree.
One possibility to accomplish
this level of placement accuracy is to first use the STM to create a
rectangular array of atoms at ca. 1 nm spacing. Then use this as a mask to
create spacing of atomic to subatomic distances. We would suffuse gaseous metal
over the rectangular array that would then produce, like with a negative image,
an array with spacing the size of the original atoms. So now the spacing would
be at atomic to subatomic widths. The gaseous metal once solidified would like
with a negative image form a new rectangular array with ca. 1 nm wall
thickness.
The gaseous metal may need to
be ionized of the same charge as the originally placed atoms so that they do
not stick to them as they cool.
Atom size spacing would be at
about 1 angstrom, 1/10th of a nm. But we might be able to get it at subatomic spacing.
For the original atoms forming the mask, we would use ionized atoms with their
outer electrons stripped off. It might be too difficult to use fully ionized
atoms, i.e., the actual positively charged nuclei, because of their small size
and the intense electric charge trying to push them apart.
But using an argon ion for
example we could get an electron radial distance of 2 pm, so an ion diameter
and spacing of 4 pm:
Atomic
Radii
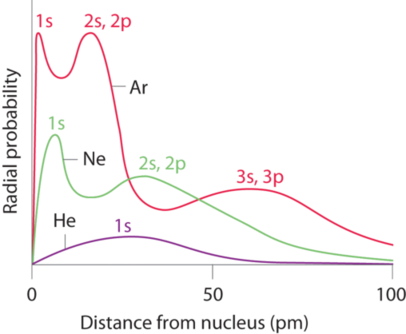
Recall
that the probability of finding an electron in the various available orbitals
falls off slowly as the distance from the nucleus increases. This point is
illustrated in Figure 7.3.1 which shows a plot of
total electron density for all occupied orbitals for three noble gases as a
function of their distance from the nucleus. Electron density diminishes
gradually with increasing distance, which makes it impossible to draw a sharp
line marking the boundary of an atom.
Figure 7.3.1: Plots of Radial Probability as a Function of Distance
from the Nucleus for He, Ne, and Ar. In He, the 1s electrons have a maximum radial probability at
≈30 pm from the nucleus. In Ne, the 1s electrons have a maximum at ≈8 pm, and the 2s and 2p electrons
combine to form another maximum at ≈35 pm (the n = 2 shell). In Ar, the 1s electrons have a maximum at ≈2 pm, the 2s and 2p electrons
combine to form a maximum at ≈18 pm, and the 3s and 3p electrons
combine to form a maximum at ≈70 pm.
Some first attempts have been
made to achieve superconductivity through individual placement of atoms:
MARCH
3, 2020
Manipulating atoms to make better superconductors
by
Natasha Wadlington, University of Illinois at Chicago
Cobalt atoms (red) are placed
on a copper surface (green) one at a time to form a Kondo droplet, leading to a
collective pattern that is the fundamental building block of superconductivity.
Credit: Dirk Morr
Scientists
have been interested in superconductors—materials that transmit electricity
without losing energy—for a long time because of their potential for advancing
sustainable energy production. However, major advances have been limited
because most materials that conduct electricity have to be very cold, anywhere
from -425 to -171 degrees Fahrenheit, before they become superconductors.
A new
study by University of Illinois at Chicago researchers published in the
journal Nature Communications shows that it is possible to
manipulate individual atoms so that they begin working
in a collective pattern that has the potential to become superconducting
at higher temperatures.
These still have only about 1
nm spacing between the atoms though, so on these as well we need methods to
achieve atomic to subatomic spacing.
We have an additional problem also
though. While positioning of atoms through the STM has been done in 2-dimensions
since the 90's, in 3-dimensions this has only been done more recently and not
with as much positional accuracy.
But for either a superluminal
communication fiber or superconducting fiber to be operational in practice you
want more than just a single atomic thickness. One possibility is that atoms
have been placed on single-atomic layer graphene as the substrate. Then
multiple layers of these each with their attached atom or ion arrays could be
placed one atop the other.
STM's are now common in many
university physics and chemistry labs. So either the superluminality or
superconductivity possibilities could be testable in many labs. However, for
the superluminality tests, since the STM produced atomic arrays are initially
likely to be small, the test of the speed of the signals would have to be
within the femtosecond range. Not many labs have time measurement devices of
this accuracy.
Easier then would be to test
the superconductivity possibility. Remarkably, there now even DIY constructed
STM's made by amateurs for which this may be even be testable on:
DIY Scanning Tunnelling
Microscope
IV.)Implications and Ramifications.
The possibility of quantum
mechanics having an interpretation in terms of superluminal speeds has
important ramifications. Actually, this has been known since the fifties with
the Bohmian interpretation of QM:
This interpretation however
does require superluminal speeds, and with such not being observed it was not
the preferred viewpoint. However, if superluminal speeds are actually observed
this or other non-local theories become preferred.
One advantage it would provide
is a reduction in the number of subatomic particles required: separate
antimatter particles would no longer be needed. Wheeler and Feynman once
proposed that the antimatter electron, the positron, was really just an
electron going back in time.
This dovetails with the idea
of superluminal speeds since the usual view of relativity is that superluminal
speeds would require signaling backwards in time. However, with the
reinterpretation of relativity by Reichenbach, superluminal speeds would not
necessarily require backwards in time signaling if using a non-standard, i.e.,
not using light signals, method of clock synchronization. This could be
provided when we have arbitrarily fast superluminal communication.
Perhaps not realized at the
time when Wheeler and Feynman proposed their backwards in time positron, is
that if using light-signal synchronization bodies that are faster-than-light
would give the appearance of traveling back in time. See the
discussion here:
Einstein, Relativity and Absolute
Simultaneity (Paperback)by William Lane Craig, Quentin Smith.
Then in such a scenario
particles and signals are not traveling backwards in time, but only give
that appearance due to an inaccurate clock synchronization method.
Then when we observe
electron-positron annihilation, what's really happening is the electron breaks
the local vacuum speed of light, thus generating vacuum Cherenkov radiation, The
electron then proceeds away at superluminal speed once it
breaks the light-speed barrier. This is what we interpret as a positron
traveling towards the "collision point".
This also explains why we see
so much more normal matter than antimatter, superluminal speeds are uncommon.
Much research now is being
devoted to quantum computers, with the prospect of orders of magnitude increase
in our ability to solve calculational problems. The same can be said of
superluminal computers if they are created.
An important class of
computationally complex problems are known as non-polynomial(NP) problems. Some
for example have known exponential time solutions. They are believed to be more
complex to solve than problems which can be solved in polynomial time. But one
of the most important unsolved problems in math and computer science is
to prove that they can not be solved in polynomial time. This
is the basis of the "P=NP?" problem.
If arbitrarily fast signaling
is possible then we may be able to do an end-around to the issue. Even if
problems do in fact require exponential time we may be able to solve them in
practical times.
A nice intro to the issues of
"P=NP?" is given in this video:
I like how she describes the
prospect of having this much computing power at our disposal at about the 13:20
point in the video.
Bob Clark






.jpg)

