Copyright 2015 Robert Clark
In the blog post
"The Coming SSTO's: Applications to interplanetary flight" I calculated that IF we have propellant depots at both departure and arrival points then a
single Falcon 9 first stage could do ALL the propulsive steps for a flight to Mars, from the LEO departure, to insertion into low Mars orbit, to Mars landing, to Mars liftoff, to departure back towards Earth.
The argument there was that this was another key advantage of SSTO's that they would have this capability. But it is important to note that this would be true for all the currently existing medium lift first stages at ca. 20 metric ton (mT) dry mass (without their needing to be SSTO), from the Atlas V, to the Delta IV, to the Soyuz, to the Ariane 5 core, to the Long March 2F, to the H-II. Then all the current spacefaring nations would have the ability to do manned Mars missions with currently existing rockets IF propellant depots are already in place. This is compared to the ca. 1,000 metric ton (mT) total mass estimates for the NASA Mars Design Reference Architectures.
Interestingly, when you consider the delta-v requirements for flights to the Moon, Venus, Mercury, and near Earth asteroids then this would also be true for these destinations with propellant depots already in place, perhaps at their Lagrange points. See for instance the Excel spreadsheet describing the Hohmann transfer flights linked on Hop David's page
Cosmic Train Schedule. Then propellant depots make possible the long desired goal of Solar System colonization, at least within the inner solar system.
The Mars flight described in "The Coming SSTO's: Applications to interplanetary flight" using single F9 stage would be flying the usual Hohmann transfer orbit of several months duration. The problems of such space trips in BEO space for several months have been much discussed, from bone and muscle loss, to radiation damage, to the recently discovered eye damage. In fact William Gerstenmaier, head of NASA's human spaceflight division, has said the NASA Mars mission architectures that might take 900 days total round trip are unworkable:
Yes, NASA really is reconsidering the moon, and here’s why that’s important.
Posted on April 6, 2015 | BY ERIC BERGER
http://blog.mysanantonio.com/newswatch/2015/04/yes-nasa-really-is-reconsidering-the-moon-and-heres-why-thats-important/
Gerstenmaier suggested, as have many others outside of NASA, that using lunar derived fuel in orbital propellant depots would make Mars missions easier and cheaper. But what has not been discussed is that with propellant depots in orbit the flight times can be cut down from the months long duration to only weeks long. That is, flight times that were thought would need advanced propulsion such as
VASIMR plasma or nuclear propulsion could be done by chemical propulsion alone, and in fact using
currently existing chemical propulsion stages.
Lightweight Habitat Modules.
A key fact that needs to be kept in mind is that when the flight times are much shorter then you can use smaller, lighter habitats that need to be transported. This results in a smaller flight vehicle. We can show once again using a single medium-lift first stage we can send a ca. 6 mT habitat to Mars in about 35 days.
Phoenix: A Low-Cost Commercial Approach to the Crew Exploration Vehicle.
http://rascal.nianet.org/wp-content/uploads/2015/07/2006-RASC-AL-UMD-Tech-Paper.pdf
This has a pressurized volume of 30 cubic meters with food, air, and water for a crew of 3 for 12 days at a ca. 2 metric ton (mT) dry mass. So putting three together will give enough consumables for the 3 crew for 36 days at a 90 m
3 volume and 6 mT mass.
Calculation of flight time to Mars using the Oberth Effect.
Another advantage of having propellant depots in cis-lunar space such as at L2 and departing from there is the
Oberth effect. This is the increase in the rockets delta-v you can get by falling deep into the departure planets gravity well and firing the engines at closest approach. I like this explanation of the effect in Robert Heinlein's book
The Rolling Stones:
A gravity-well maneuver involves what appears to be a contradiction in the law of conservation of energy. A ship leaving the Moon or a space station for some distant planet can go faster on less fuel by dropping first toward Earth, then performing her principal acceleration while as close to Earth as possible. To be sure, a ship gains kinetic energy (speed) in falling towards Earth, but one would expect that she would lose exactly the same amount of kinetic energy as she coasted away from Earth.
The trick lies in the fact that the reactive mass or 'fuel' is itself mass and as such has potential energy of position when the ship leaves the Moon. The reactive mass used in accelerating near Earth (that is to say, at the bottom of the gravity well) has lost its energy of position by falling down the gravity well. That energy has to go somewhere, and so it does - into the ship, as kinetic energy. The ship ends up going faster for the same force and duration of thrust than she possibly could by departing directly from the Moon or from a space station. The mathematics of this is somewhat baffling - but it works.
http://www.projectrho.com/public_html/rocket/mission.php#id--Oberth_Effect
On that www.projectrho.com page is given this formula for calculating the Oberth effect:
To actually calculate the bonus delta V you will get from the Oberth Maneuver:
Vf = sqrt((Δv + sqrt(Vh2 + Vesc2))2 - Vesc2)
Δv = sqrt(Vf2 + Vesc2) - sqrt(Vh2 + Vesc2)
where:
Vf = final velocity (m/s)
Vh = initial velocity before Oberth Maneuver(m/s)
Δv = amount of delta V burn at periapsis (m/s)
Vesc = escape velocity at periapsis (m/s)
For the propulsion stage we'll use the
Ariane 5 "G" core. This has 158 mT propellant load and 12 mT dry mass at 434 s Isp engine. We'll make some small modifications to increase performance. The Ariane 5 core launches from ground so has a intermediate size nozzle to operate at sea level and vacuum. For our use, we're only using it for vacuum so we'll give it a nozzle extension such as on the
RL-10B2 Centaur engine to increase the Isp to 462 s. We'll also remove a forward skirt on the core called the
"JAVE", from the French "Jupe AVant Equipée", that is used to attach the solids to the Ariane 5. This massed 1,700 kg, bringing the dry mass now down to 10,300 kg.
Then this can produce an Isp with a 6 mT payload of:
462*9.81ln(1 + 158/(10.3 + 6)) = 10,700 m/s = 10.7 km/s.
Now use the Oberth effect to calculate the speed after the periapsis burn:
V
f = sqrt((10.7 + 11.1)
2 - 11.1
2) = 18.8 km/s.
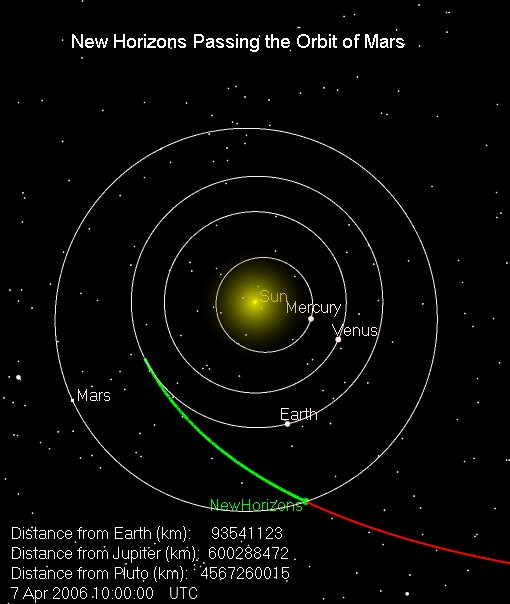
For departure speeds this high the trajectory is nearly straight-line despite the influence of the Sun. The New Horizons mission gives an example of fast travel times possible with chemical propulsion:
Pluto-Bound Probe Passes Mars’ Orbit.
by Tariq Malik, Staff Writer | April 07, 2006 01:45pm ET
"It's pretty amazing," New Horizons principal investigator Alan Stern told SPACE.com. "It's a straight line across the Solar System. There are hardly any curves because this is so fast."
New Horizons sped past Mars' orbit some 151 million miles (243 million kilometers) from the Sun at a rate of about 13 miles (21 kilometers) per second. The red planet, however, trailed behind the spacecraft at a distance of about 186 million miles (299 million kilometers), mission managers said, adding that New Horizons was closer to Earth than Mars.
http://www.space.com/2263-pluto-bound-probe-passes-mars-orbit.html
Passing the Orbit of Mars.
New Horizons' trailblazing journey to the solar system's outermost frontier took it past the orbit of Mars at 6 a.m. EDT (1000 UTC) on April 7, 2006 - 78 days after the spacecraft launched.
http://pluto.jhuapl.edu/Mission/Where-is-New-Horizons/Passing-Planets/Passing-Planets-Mars.php
The distance between Mars and Earth at the time was about 90 million km. The 2018 Mars opposition on the other hand is a particularly close approach at about 58 million km away. At that time for New Horizons to make the trip would have been about 48 days.
Our flight would be at a faster speed of 18.8 km/s compared to the 12 km/s of New Horizons. Then for the close 2018 opposition, the approximate flight time would be 58,000,000/(18.8*3,600*24) = 35.7 days. This from using a
single Ariane 5 core stage, launched dry, fueled at an L2 propellant depot.
Fuel for the propellant depots.
Because of its proximity the Moon has been often offered for the fuel source for the orbital propellant depots. This would be simpler if the process needs to be supervised by humans. However, some near Earth asteroids have a much smaller delta-v and very much smaller gravity for delivering the fuel to the cislunar system:
Asteroid Retrieval Feasibility Study.
2 April 2012
http://kiss.caltech.edu/study/asteroid/asteroid_final_report.pdf
Much of the discussion of retrieving asteroids has been about the solar electric ion propulsion used and that perhaps it would cost $2.6 billion to develop. But I was surprised in the report that it also discussed doing it with LH2/LOX chemical propulsion and how little propellant it would use. First it notes that an asteroid such as 2008HU4 at closest approach would require only a 170 m/s (!) delta-v to bring it to lunar orbit. Then in figure 19 on p. 43 is given a comparison between the propellant required for LH2/LO2, N204/MMH, and SEP propulsion for this asteroid at an assumed 1,000 mT mass.
Surprisingly, for the LH2/LO2 case it is less then 40 mT for a 1,000 mT payload! This is because of course it is only a 170 m/s delta-v. But this means for the 500 mT case that was initially cited for the mission it would be less than 20 mT propellant load, and a LH2/LOX propulsion stage this size is already available in the Centaur. Note also that at an only 170 m/s delta-v to get the Centaur to this asteroid, you would only need to use about 1 mT out of the 20 mT propellant load.
Since the chemical propulsion would have greater thrust, the mission return time would also be significantly less than the 10 years for the SEP propulsion.
Planetary Resources, Inc. is launching small telescopes to prospect for asteroids either for mineral resources or for water for propellant. Many asteroids or extinct comets will have large amounts of water ice. Rather than using many rovers to scoop up the surface material for processing, there is an easier approach. Parabolic trough mirrors could be positioned around the four sides of a rectangle on the surface and angled inwards to cut out an upside down triangular prism shaped portion of the asteroid.
 |
| Parabolic trough mirror. |
 |
| Triangular prism. |
Because of the low gravity of the asteroid the water and dust vaporizing will tend to lift the block off the surface.
Another possibility would be to use microwaves to evaporate the water ice:
Microwaving Water from Moondust.
October 7, 2009.
"We believe we can use microwave heating to cause the water ice in a lunar permafrost layer to sublimate – that is, turn into water vapor. The water vapor can be collected and then condensed into liquid water."
"Best of all, microwave extraction can be done on the spot. And it requires no excavation -- no heavy equipment for drilling into the hard-frozen lunar surface."
He calls his first mining experiment the "Moon in a bottle."
"We filled a bottle with simulated lunar permafrost [fake moondust containing water ice] and heated it in a microwave oven. The microwaves heated the simulant enough to extract water, even though the soil was as cold as it would be on the Moon."
At least 95 percent of the water added to the simulant was extracted (vaporized out of the soil) with 2 minutes of microwaving.
"And we were able to capture 99 percent of the vaporized water in our cold trap," says collaborator Bill Kaukler of the University of Alabama-Huntsville. "It works."
http://science.nasa.gov/science-news/science-at-nasa/2009/07oct_microwave/
This method of using microwaves was proposed instead of direct heating with sunlight because the lunar regolith does not have very good thermal conductivity and much of the heat would just be re-radiated back. However, the conversion from solar cells to electricity is only about 30% efficient, and the conversion from electricity to microwaves is only about 70% efficient, so this would only be about 21% efficient conversion of the solar energy to the water ice.
Instead we could cover the area to be illuminated by a dark, non-reflecting material that was reflecting on the reverse side. We would also want it to have good thermal conductivity. Then the heat would be communicated throughout the surface to the regolith/ice below and re-radiated heat from the regolith would be reflected back down into the surface. You could make it be porous so the water vapor could escape.
In both cases the microwave and the direct sunlight you would cover the area with an enclosing shroud to collect the water vapor that evolved.
All of these methods could be used on asteroids, the Moon, Mars, and the moons of Mars to collect propellant for orbital propellant depots.
Another possibility is to use the outgassed volatiles from near Earth comets or cometary fragments:
Dust Whirls, Swirls and Twirls at Rosetta’s Comet.
by BOB KING on MARCH 9, 2015
http://www.universetoday.com/119296/dust-whirls-swirls-and-twirls-at-rosettas-comet/
The advantage is no landing or solar heating equipment would be required. You could just collect the released H2O, and CO2, CO for hydrocarbon fuel, from orbit. You might want though to enclose the entire comet in a shroud to capture all the released volatiles, as just collecting from orbit would miss most of the released volatiles.
Reentry at Mars.
These fast travel times using a single medium-lift first stage allow no propellant to slow down. Moreover because of their high travel speed, they will arrive at higher velocity than the normal Hohmann transfer velocity. The Hohmann transfer flight would have a reentry speed of ca. 6 km/s. But with the high transit speeds of 30 day flight duration, the Mars reentry speed might be ca. 20 km/s(!)
Then new methods would be needed to allow the spacecraft to slow down and land on Mars. In follow-up posts I'll describe various methods of achieving this, from high lift/drag ratio hypersonic airfoils, to ultra lightweight parashields, to magnetoshells, to combusting components of the Martian atmosphere, to expelled propellant forming a cooling gaseous blanket to the reentry heat.
Bob Clark